Optimizing Kerbal life support with linear fractional programming

Kerbal Space Program is one of my favorite games of all time. It allows the player to build and fly rockets on missions all around the Kerbal solar system. It simplifies many of the detailed complexities of planning space missions, and in doing so creates a whole ‘solar system’ of toy problems to solve, such as finding the optimal engine for a given rocket stage or the optimal rocket to lift a payload. In this post I’ll introduce (Mixed-integer) Linear Fractional programming, a variant of linear programming, to optimally choose the parts needed for a mission.

The base KSP game lacks a concept of ‘life support’ requirements. These are added by a mod called, appropriately, USI Life Support. Kerbals now consume a resource called ‘Supplies’ over time, and they need to pack enough Supplies for the length of their missions or else they become hungry and refuse to work. There are also two kinds of ‘Recycler’ parts (‘Small’ and ‘Large’) which lower the rate of Supplies consumption.

Problem statement

Minimizing mass is important for launching missions to space. For a mission with a certain number of Kerbals, what is the lowest mass required to provide Supplies for a certain number of days, and how many Supplies, Small Recyclers, and Large Recyclers should make up that mass?

Kerbal Supplies storage, consumption and recycler rules

The base rate of Supplies consumption is $s_d = 10.8$ kg/day per Kerbal. Supplies are stored in several sizes of tins which are ⅚ Supplies by mass when full. The smallest sized tin is just 120 kg when full, so for this post we’ll consider Supplies to be a ‘continuous’ resource.

The two Recycler parts each affect a certain number of Kerbals.

• The Small Recycler reduces the rate of Supplies consumption by $s_{r,S} =$ 60% for one Kerbal and has a mass of $m_S = $0.1 tons.
• The Large Recycler reduces the rate of Supplies consumption by $s_{r,L} =$ 79% for up to three Kerbals and masses $m_L$ 3.75 tons.

Each Kerbal can only be assisted by one recycler, and it will choose the one that most decreases its consumption (assuming that the recycler has a free slot). A ship can have multiple recyclers in order to serve multiple Kerbals.

There are additional mechanics in USI-LS (Habitation requirements, and fertilizer and agroponics to grow more Supplies) but this post will not consider them further.

Problem formulation

Rather than solve for the minimum mass to supply $n_K$ Kerbals for $d$ days, we solve for the maximum number of days $d$ on which they can survive for a given life support mass budget $m_\mathrm{tot}$. This turns out to be equivalent but is easier to formulate. Our decision variables are the numbers of small and large recyclers, $n_S$ and $n_L$, respectively.

The number of days they can survive is just the mass of supplies divided by their rate of consumption, so the objective is

The mass of supplies is $(5/6)(m_\mathrm{tot} - n_S m_S - n_L m_L)$. The rate of consumption is a bit more difficult to write correctly, since the Large Recycler applies to up to three Kerbals. This is a nonlinear behavior. As a first approximation, we will consider a system where the Large Recycler can be divided into three parts, each of which applies to only one Kerbal. Call the number of these $n_{L_3^1}$ and their mass $m_{L_3^1} = m_{L} / 3$.

The rate of consumption is then $s_d (n_K - s_{r,S} n_S - s_{r,L} n_{L_3^1})$, and the mass of supplies is $(5/6)(m_\mathrm{tot} - n_S m_S - n_{L_3} m_{L_3^1})$ The constraints are nonnegativity,

$ n_S \ge 0, \quad n_{L_3^1} \ge 0$;

and that the number of recyclers (or partial recyclers) should not exceed the number of Kerbals,

$ n_S + n_{L_3^1} \le n_K$.

This prevents the Supplies consumption rate from being negative.

Solution to the first approximation

The objective matches the form required for Linear Fractional Programming (LFP):

where $\alpha = \frac{5}{6}(-m_S, -m_{L_3^1})$, $\beta = \frac{5}{6}m_\mathrm{tot}$, $\gamma = -s_d \left(s_{r,S}, s_{r,L}\right)$, $\delta = s_d n_K$, and $x = (n_S, n_{L_3^1})$. The constraints are all linear functions of the input variables as well. This means that the problem can be solved by LFP. This is good, because LFP problems are easy to solve. They can be transformed into standard Linear Programming (LP) problems automatically. However, this is also an Integer Programming problem, since the number of small recyclers and large recyclers must be an integer. This means our problem is in ILFP, Integer Linear Fractional Programming.

Removing the approximation

We need to figure out some way to keep the problem formally linear, while capturing the nonlinear behavior that a Large Recycler has the same mass whether it applies to one, two, or three Kerbals. We do this by splitting the Large Recycler into three varieties, each of which has the full mass: one which applies to one Kerbal, one which applies to two, and one which applies to three. We’ll call these $n_{L1}$, $n_{L2}$, and $n_{L3}$, respectively. The solution will avoid situations where there are both $n_{L1} > 0$ and $n_{L2} > 0$, since the two could be combined into an $n_{L3}$ while saving mass.

The decision variable vector $x$ is $\left(n_S, n_{L1}, n_{L2}, n_{L3}\right)$.

The mass of Supplies is

and the rate of their consumption is

The constraint on the number of recyclers becomes

\(n_S + n_{L1} + 2 n_{L2} + 3 n_{L3} \le n_K\).

Solution using Mathematica

Solving this ILFP with Mathematica is especially easy because it has a built-in function LinearFractionalOptimization.

Here is a Mathematica function to solve the problem. nKerbals is an integer and the massBudget is in tons.

sd = 0.0108 (*tons per day per kerbal*);
suppToTot = 5/6 (*Ratio of supplies to total mass*);
mS = 0.1 (*tons*);
mL = 3.75 (*tons*);
srs = 0.6 (*supply reduction for the Small Recycler*);
srl = 0.79 (*supply reduction for the Large Recycler*);

longestDurationLFO[nKerbals_, massBudget_] := 
 Module[{masses, α, β, γ, δ, ac1, bc1, sol, x, 
   xsol, positivityConstraint, massBudgetConstraint, 
   kerbalsServedConstraint, constraints, mSupp, days, largeRec}, 

  masses = {mS, mL, mL, mL};
  α = -suppToTot masses;
  β = suppToTot massBudget;
  γ = -sd {srs, srl, 2 srl, 3 srl};
  δ = sd nKerbals;

  ac1 = {1, 1, 2, 3} (*kerbals served per recycler*);
  bc1 = nKerbals;
  
  positivityConstraint = VectorGreaterEqual[{IdentityMatrix[4].x, 0}];
  massBudgetConstraint = masses.x <= massBudget;
  kerbalsServedConstraint = ac1.x <= bc1;
  constraints = {positivityConstraint, massBudgetConstraint, 
     kerbalsServedConstraint};
  
  sol = LinearFractionalOptimization[-(α.x + β)/(γ.x + δ),
    constraints, {x ∈ Vectors[4, Integers]}];

  (*postprocessing*)
  
  xsol = x /. sol;
  mSupp = α.xsol + β;
  days = mSupp/(δ + γ.xsol);
  largeRec = Total[xsol[[2 ;;]]];
  <|"Supplies/kg" -> 1000 mSupp, "SmallRec" -> xsol[[1]], 
   "LargeRec" -> largeRec, "Days" -> days|>
]

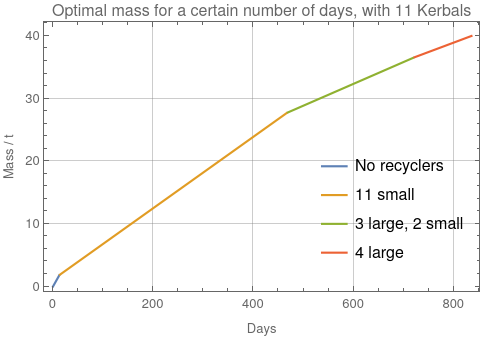
Example chart of optimal mass for 11 Kerbals

Figure 1 shows the smallest mass and number of recyclers of each type required to support $n_K = 11$ Kerbals for a certain number of days. The optimal solution takes the form of several line segments. For $n_K$ evenly divisible by three there are three segments, corresponding to no recyclers, one small recycler per Kebal, and one large recycler per three Kerbals. For $n_K > 3$ and not evenly divisible by three there are four segments, such as seen in Figure 1.

(Lack of) a quick solution using open-source software

Unfortunately python’s scipy.optimize only has a linear programming engine linprog built in; it doesn’t solve even LFP or (mixed) integer linear programming problems (ILP or MILP). There is relatively simple way to transform a LFP problem to an LP problem (the ‘Charles-Cooper transformation’) but it’s more complex to transform ILFP into ILP, and a library like pyomo plus a solver would be required.

Alternately, for this problem it’s pretty easy to enumerate all the reasonable combinations of recyclers, find the linear relationships between days of supplies and total mass that each leads to, and find the lowest mass from these linear relationships. However, that technique might be more difficult if the complexity of the program were to increase, for example, if more types of recyclers were included.

Future work: inclusion of Agroponics modules

So far I’ve only explored three elements of USI Life Support: the Supplies containers and the Small and Large Recyclers. However, there is another class of element: the Agroponics module, which turns Fertilizer and Mulch into Supplies. These should substantially reduce the mass required, leading to better solutions. The optimal life support system including these should be explored in future work.