Jacob Schwartz Scientist & HTML fan
Radial profiles of deposition in a cylinder

An infinite cylinder of radius $1$ is surrounded by a uniform, isotropic, collisionless gas of particles. When particles enter the cylinder region, they are absorbed with some mean free path $\lambda$. I provide an expression for the radial profile of absorption (deposition) intensity $i(\rho, \lambda)$
This is the third post in a series. The previous two examined 2D version of this geometry—a disk in a plane—and calculated the fraction of particles that survive crossing the disk, and the radial profile of the deposition intensity.
\[\newcommand{\cancelcolor}[1]{\color{red}{#1}} \newcommand{\gone}[1]{\color{midnightblue}{#1}} \newcommand{\gtwo}[1]{\color{forestgreen}{#1}} \newcommand{\gthree}[1]{\color{crimson}{#1}} \newcommand{\gfour}[1]{\color{purple}{#1}} \newcommand{\ki}[2]{\mathrm{Ki}_{#1}\left(#2\right)}\]Set up the integral
I want to find the volumetric intensity of deposition at a given radius $\rho$, which I will call $i(\rho, \lambda)$. This is the total deposition per unit length and per unit time in the cylindrical shell of radius $\rho$ and width $d\rho$.
The deposition intensity is
\[\begin{equation} i(\rho, \lambda) = \frac{\int_{\beta=0}^\pi \,d\beta \int_{\phi=0}^{2\pi}\sin\beta \,d\phi}{4\pi} \frac{\int_{\theta=0}^{2\pi}\,d\theta \rho \,d\rho \sin\beta\; y(\phi, \theta, \beta, \rho, \lambda)}{2\pi\rho \,d\rho}, \tag{1}\label{eq:setup} \end{equation}\]where $y(\phi, \theta, \beta, \rho, \lambda)$ is the contribution from particles moving at horizontal angle $\phi$, located at cylindrical polar angle $\theta$, moving with angle from the pole $\beta$, at radius $\rho$, and with mean free path $\lambda$. The two integrals in the first part sum over all angles of particle motion. The $\sin\beta$ there is the standard Jacobian of spherical coordinates. The second term averages the deposition over the volume of the cylindrical shell at radius $\rho$ with width $d\;\rho$. The $\sin\beta$ here accounts for the flux of particles into the cylinder shell, which is higher at $\beta$ far from the cylinder axis.
We resolve the integral over $\phi$ by symmetry: after averaging over the cylinder polar angle $\theta$, the contribution from all $\phi$ will be the same, that is,
\[\int_0^{2\pi}\,d\theta\int_0^{2\pi} \,d\phi\, y(\phi, \theta, ...) = 2\pi\, \int_0^{2\pi}\, d\theta\, y(\phi=\pi, \theta, ...)\]where I’ve chosen $\phi=\pi$ to align with the image (Figure 1) of particles moving leftward into a cross section of the cylinder.
Thus, cancelling a $2\pi$ and the $\rho$ and $d\rho$, and combining the two $\sin\beta$ terms,
\[\begin{equation} i(\rho, \lambda) = \frac{1}{4\pi}\int_{\beta=0}^\pi \,d\beta \sin^2\beta \int_{\theta=0}^{2\pi}\,d\theta \, y(\phi=\pi, \theta, \beta, \rho, \lambda). \tag{2}\label{eq:two} \end{equation}\]
For particles coming from a given $\phi$ and $\beta$, the deposition intensity $y$ at the point given by $(\rho, \theta)$ is
\[y = \frac{1}{\gone{\lambda \sin\beta}}\exp(-d_\mathrm{decay}/\lambda),\]where
\[d_\mathrm{decay} = \left(\sqrt{1 - \rho^2\sin^2\theta} - \rho \cos \theta\right)/\sin\beta.\]The leading $\gone{1/(\lambda\sin\beta)}$ is the intensity of deposition from particles with mean free path $\lambda$ combined with the fact that particles travel across the cylinder at a speed proportional to $1/\sin\beta$. So all together (and splitting $4\pi$ into $2$ and $2\pi$),
\[\begin{equation} i(\rho, \lambda) = \frac{1}{2}\int_{0}^{\pi}\,d\beta \sin^2 \beta \int_0^{2\pi}d\theta\; \frac{1}{2 \pi \lambda \sin \beta} e^{-\left(\sqrt{1 - \rho^2 \sin^2\theta} - \rho \cos\theta\right)/\lambda \sin\beta}. \tag{3}\label{eq:three} \end{equation}\]Relating to the 2D problem
This intensity can be expressed as an integral over $\beta$ of the solution to the problem of the previous post in the series, $i_\mathrm{disk}$:
\[\begin{equation} i_\mathrm{cyl}(\rho, \lambda) = \frac{1}{2}\int_0^{\pi}\,d\beta \sin^2\beta \;\; i_\mathrm{disk}(\rho, \lambda \sin \beta). \tag{4}\label{eq:relateToCyl} \end{equation}\]Intuitively, the radial profile of deposition from particles with $\lambda=1$ moving at an angle where $\sin\beta = 1/2$ is the same as from particles moving horizontally ($\sin\beta = 1$) with $\lambda = 1/2$.
Integrate each term in the Taylor series
We recall the disk problem’s solution in the form of a Taylor series, and substitute $\lambda \to \lambda \sin \beta$:
\[i_\mathrm{disk}(\rho, \lambda \sin \beta) = \frac{1}{2 \lambda \sin\beta} \sum_{\mathrm{even}\,n \ge 0} \frac{\rho^2}{n!} \sum_{k=0}^{n-1} \frac{u_{n,k}}{(\lambda \sin \beta)^{n-k}}e^{-1/\lambda \sin \beta}\]The ratio $u_{n,k}$ was derived in the previous post; it is reprinted at bottom.
where $u_{n,k}$ is a ratio of integers given by a complicated expression.
To proceed with $i_\mathrm{cyl}$ we move the integral over $\beta$ inside both sums—it is independent of the counters $n$ and $k$—combine the powers of $\sin\beta$, and move the power of $\lambda$ in front of the integral, yielding
\[\begin{equation} i_\mathrm{cyl} = \frac{1}{4\lambda} \sum_{\mathrm{even}\,n \ge 0} \frac{\rho^2}{n!} \sum_{k=0}^{n-1} u_{n,k} \frac{1}{\lambda^{n-k}} \int_0^{\pi} \frac{e^{-1/\lambda \sin \beta}}{\sin^{n-k-1} \beta}\,d\beta. \tag{5}\label{eq:five} \end{equation}\]The integral can be expressed in terms of an obscure special function, the Bickley-Naylor function $\mathrm{Ki}$.
Express integral with a special function
The Bickley-Naylor function1 is defined as
\[\ki{m}{x} \equiv \int_0^{\pi/2} e^{-x/\cos\theta}\cos^{m-1}\theta\;d\theta.\]To match $\int_0^\pi (\ldots) e^{-1/\lambda \sin\beta}\;d\beta$ we perform some elementary manipulations: change $x$ to $1/\lambda$, replace $\theta$ with $\beta$, replace the $\cos$ with $\sin$ (equal, by symmetry) and extend from $0\to\pi/2$ to $0\to\pi$ (double, by symmetry). Thus
\[\int_0^{\pi} \frac{e^{-1/(\lambda\sin\beta)}}{\sin^m\beta}\;d\beta = 2\mathrm{Ki}_{1-m}\left(\frac{1}{\lambda}\right).\]The solution
The deposition intensity is
\[\begin{equation} \boxed{ i(\rho, \lambda) = \frac{1}{2 \lambda} \sum_{\mathrm{even}\,n \ge 0} \frac{\rho^n}{n!} \sum_{k=0}^{n-1} \frac{u_{n,k}}{\lambda^{n-k}} \mathrm{Ki}_{2 + k -n}\left(\frac{1}{\lambda}\right). } \end{equation}\]where (from Eq. (12) of the earlier post)
\[\begin{equation} \begin{aligned} u_{n,k} &= \frac{2} {\pi (n/2)!} \sum_{c=\max(0,\,k-n/2)}^{k/2} (2k-2c-1)!! \\ & \frac{(k-2c)_{2c}}{2^c\,c!} \binom{n}{n+2c-2k} \Gamma \left(\frac{1}{2}-c+k\right) \Gamma \left(\frac{1}{2}+c-k+\frac{n}{2}\right). \end{aligned} \end{equation}\]Plots of $i(\rho,\lambda)$
The left half of Figure 2 shows plots of ${i}(\rho, \lambda)$ at various $\lambda$ and the right half shows the accuracy of Taylor series out to various orders.
Other than the Taylor series traces, these plots were computed with numerical integration of Equation (3).
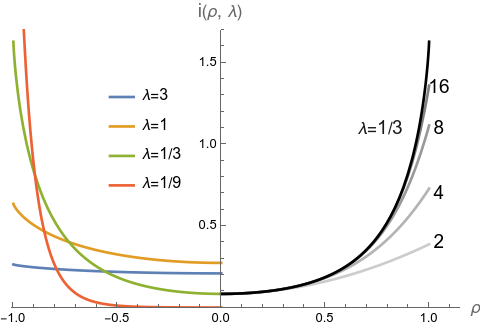
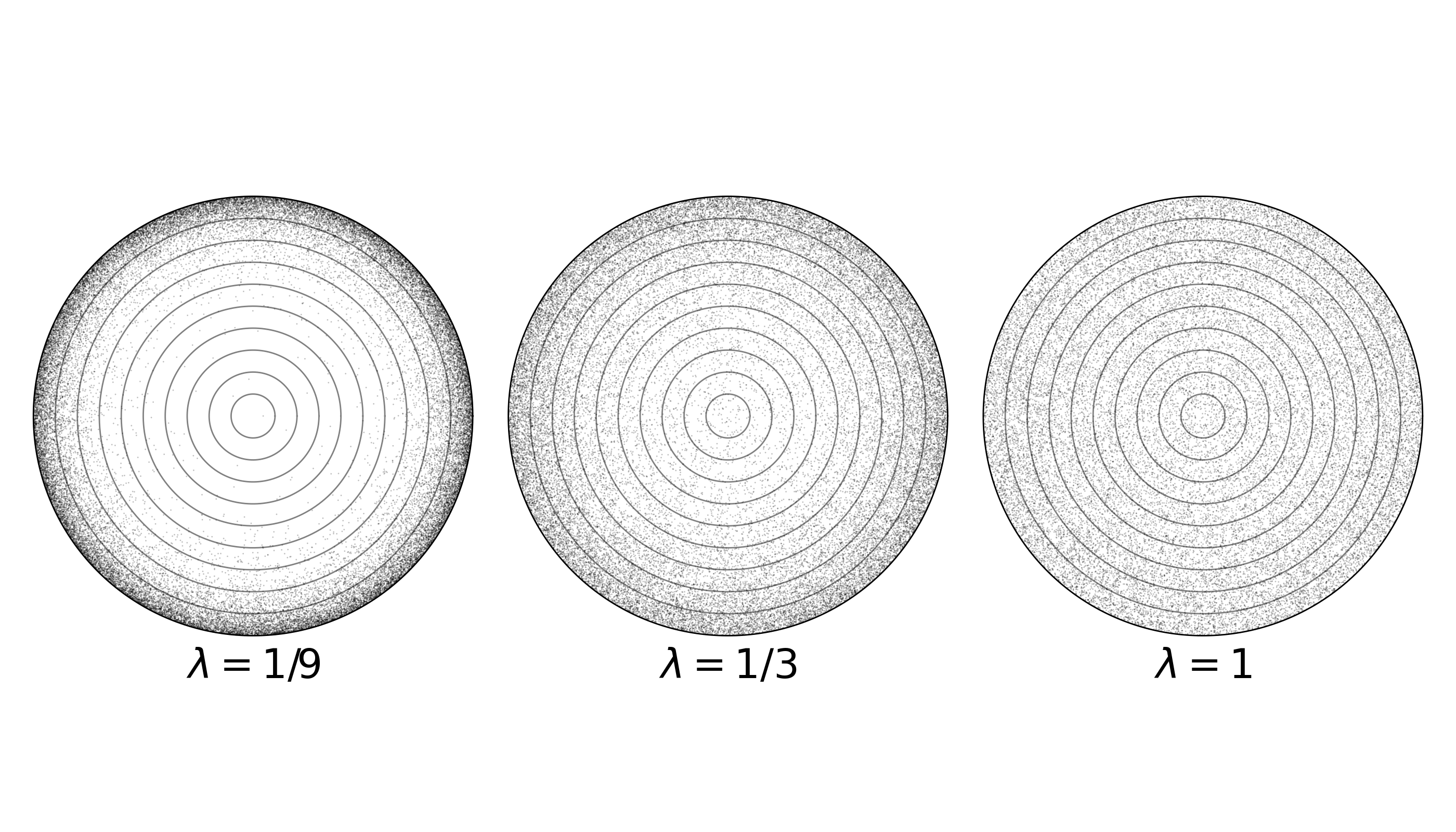
Figure 3 shows the results of a numerical simulation2 at three values of $\lambda$.
Special cases: intensity at the edge and center

At the cylinder edge
At $\rho=1$ the intensity reaches a value of
\[\begin{equation} i(1, \lambda) = \frac{1}{2\lambda} + \frac{\pi ^{3/2}}{4\lambda} G_{2,4}^{2,0}\left(\frac{1}{\lambda ^2}\Bigg| \begin{array}{c} \frac{1}{2},\frac{3}{2} \\ 0,1,0,\frac{1}{2} \\ \end{array} \right)-\frac{1}{\lambda ^2}. \tag{6}\label{eq:edgeintensity} \end{equation}\]This edge intensity is finite for any positive $\lambda$. At small $\lambda$ the leading $1/2\lambda$ term dominates and the function tends toward a value of, from what I can tell numerically, is like $1/(2\lambda) + 1/8$. Annoyingly I can’t prove the value $1/8$ is correct analytically. I’m unsure how to formally analyze Expression (6) in the small-$\lambda$ limit. The Meijer-G function and $-1/\lambda^2$ are the two leading terms but nearly cancel, leaving a difference very close to $1/8$.
At large $\lambda$ the intensity at the edge asymptotes to
\[\frac{1}{\lambda } -\frac{1}{\lambda ^2} +\frac{2-2 \gamma +\log (4)+2 \log (\lambda )}{4 \lambda ^3}\]where $\gamma$ is Euler’s gamma constant.
At the cylinder center
At $\rho = 0$ the deposition intensity becomes
\[i(0, \lambda) = \frac{1}{\lambda}\mathrm{Ki}_2\left(\frac{1}{\lambda}\right).\]This function has a broad maximum around $\lambda = 1.21979$ with a value of 0.278937.
At small $\lambda$ this goes like $\sqrt{\frac{\pi }{2}} e^{-1/\lambda }/\sqrt{\lambda }$, shown with the orange dotted line.
At $\lambda \gg 1$ it asymptotes to
\[\frac{1}{\lambda} -\frac{\pi }{2 \lambda ^2} +\frac{3-2 \gamma +\log (4)+2 \log(\lambda)}{4 \lambda ^3}.\]Future work
In this post I derived a solution in the form of a Taylor series around $\rho=0$. This works well near the center of the cylinder, but as $\rho \to 1$ the function curls up to a finite value (Expression (6)) with a sharp edge (the radial derivative goes to infinity). It would be interesting to explore the radial behavior as $\rho \to 1$ at fixed $\lambda$.
Acknowledgements
Thanks to J. Parisi for his encouragement of my pursuit of these expressions!
-
The Bickley-Naylor (or sometimes just Bickley) function is related to Bessel functions. See descriptions of it at Wikipedia, Wolfram, and NIST. In Mathematica, it needs to be loaded with
ResourceFunction["BickleyKi"]. To my knowledge there is no python library that defines it. ↩ -
I used this python code to generate the stippled-disc plots.
import numpy as np import matplotlib.pyplot as plt def sample_sinsquared(n_samples): """Uses symmetry to get one variate per random number""" x = np.pi/2 * np.random.rand(n_samples) y = np.random.rand(n_samples) sinsq = np.sin(x)**2 flip = sinsq < y x[flip] = np.pi/2 + x[flip] return x def random_beta(n_samples): """Returns a sin^2 distribution between 0 and pi/2 """ return sample_sinsquared(n_samples) def random_b(n): """Impact factor between -1 and 1""" return -1 + 2 * np.random.rand(n) def random_length(n, mfp): """Particle survival length. May exceed path length through cyl""" return -mfp * np.log(np.random.rand(n)) def max_x_length_b(b): """Horizontal distance across the circle at impact factor b""" return 2*np.sqrt(1-b**2) def max_acceptable_distance(b, beta): """3D length across the cylinder at impact factor b, angle β""" return max_x_length_b(b) / np.sin(beta) def end_x(b, xlength): """Final x loc for impact factor and survival length""" x0 = -np.sqrt(1 - b**2) return x0 + xlength def deporadius(*, b, beta, mfp): """Evaluate sample directions""" edgedistance = max_acceptable_distance(b, beta) n_samples = len(b) depodistance = random_length(n_samples, mfp) depo_x = np.sqrt(1 - b**2) - depodistance * np.sin(beta) depo_y = b depo_r = np.sqrt(depo_x**2 + depo_y**2) good = edgedistance > depodistance return depo_x[good], depo_y[good], depo_r[good] ############### Draw figure ################ def drawcircle(ax, radius, **kwargs): θ = np.linspace(0,2*np.pi, num=360) x = radius * np.cos(θ) y = radius * np.sin(θ) ax.plot(x, y, **kwargs) fig, axx = plt.subplots(1,3, figsize=(7,4)) for ax in axx: drawcircle(ax, 1, color='black', lw=0.5) for r in np.linspace(0.1,0.9, num=9): drawcircle(ax, r, color='gray', lw=0.5,zorder=-999) for side in ['top', 'bottom', 'left', 'right']: ax.spines[side].set_visible(False) ax.set(xticks=[], yticks=[]) ax.set_aspect(1) ax.set(xlim=[-1.01,1.01], ylim=[-1.01,1.01]) mycolor = "#00000040" for ax, mfp in zip(axx, [1/9, 1/3, 1]): n_samples = 40_000 b = random_b(n_samples) beta = random_beta(n_samples) x, y, dr = deporadius(b=b, beta=beta, mfp=mfp) # all particles come in from the right side. # here, spin them around the disk to a random angle. random_phi = 2*np.pi * np.random.rand(len(dr)) ax.scatter(dr * np.cos(random_phi), dr * np.sin(random_phi), 1, color=mycolor, marker='.', edgecolors='none', facecolors=None) axx[0].text(0,-1.05,'$\lambda = 1/9$', verticalalignment='top', ha='center', size=14) axx[1].text(0,-1.05,'$\lambda = 1/3$', verticalalignment='top', ha='center', size=14) axx[2].text(0,-1.05,'$\lambda = 1$', verticalalignment='top', ha='center', size=14) plt.tight_layout() plt.show()