Fraction of particles passing through a disk

This is a problem in 2D.

A uniform, isotropic 2D gas of particles surrounds a disk-shaped region of radius $1$. As the particles pass through the disk, they are absorbed with some typical mean free path $\lambda$. Of the particles that strike the disk, what fraction pass through it?

The setup for this problem is relatively straightforward. Since the gas is isotropic (and the disk is symmetric), we can calculate this for particles that are moving in one particular direction; the result will be independent of the direction. As the illustration shows, the particles hit the disk with some uniform-random impact parameter $b$ between $-1$ and $1$.

A particle with impact parameter $b$ must pass through a distance $l = 2 \sqrt{1-b^2}$ to the other side. The fraction that survive the distance $l$ is $\exp(-l/\lambda) = \exp(-2\sqrt{1-b^2}/\lambda)$.

Over all impact parameters, the fraction that survive is

\[f_\text{survive}=\frac{\int_{-1}^{1} e^{-2\sqrt{1-b^2}/\lambda} \; db}{\int_{-1}^{-1}\;db}=\frac{1}{2}\int_{-1}^{1} e^{-2\sqrt{1-b^2}/\lambda} \; db = \int_0^1 e^{-2\sqrt{1-b^2}/\lambda}.\]

To do this integral, substitute $x = \sqrt{1-b^2}$. Then $db = -x/\sqrt{1-x^2} \; dx$. The integral becomes

\[f_\mathrm{survive} = \int_0^1 \frac{x}{\sqrt{1-x^2}}e^{-2x/\lambda}\;dx.\]

Mathematica can do this integral; the result is

\[f_\mathrm{survive} = \frac{\pi}{2} \left(\pmb{L}_{-1}\left(\frac{2}{\lambda }\right)-I_1\left(\frac{2}{\lambda}\right)\right)\]

where $I_1$ is a Bessel function and the $\pmb{L}_{-1}$ is a modified Struve function. This combination came up previously as part of a similar integral, in this earlier post.

Plots and asymptotics

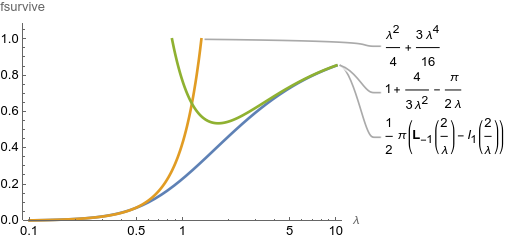
At small $\lambda$ the survival function goes like $\lambda^2/4 + 3 \lambda^4/16$.

At large $\lambda$ it goes like $1 - \pi/(2\lambda) + 4/(3\lambda^2)$.

Written on July 18th, 2024