Jacob Schwartz Scientist & HTML fan
Finding the fusion rate coefficient for a beam of fast particles in a Maxwellian background
In a future (magnetic) fusion reactor, most of the fusion reactions will occur between the nearly-thermal (i.e. isotropic Maxwellian) plasma ions. But there are also certain classes of “fast particles”, which are moving at a much higher velocity than the typical background plasma ions. These include ions formed due to Neutral Beam Injection, and also fusion products themselves. Since they are moving fast, and fusion cross sections generally increase with higher relative velocity, they can generate a non-negligible fraction of the fusion power. This is especially true for today’s experiments, where most of the fusion power may be from the fast ions of NBI injection.
In this post, I will describe how to carry out the integral to determine the rate coefficient of fusion reactions between a background plasma at temperature $T$ and a beam of fast ions with energy $E_F$. While naively one might think this requires a 3D integral (because of the three dimensions of motions of particles in the background plasma) I will show how it can be reduced to a single 1D integral.
To start, let’s define the variables: The background plasma is made of a species with mass $m_b$, and has temperature $T$. The fast ions have mass $m_F$ and energy $E_F$. Without loss of generality, we can define their direction of motion to be the $\hat{z}$ direction, with velocity $v_F$. The fusion reaction cross section $\sigma$ is a function of the center-of-mass energy $E$ between a background particle and a fast particle, $\sigma(E)$, or equivalently a function of the magnitude of their relative velocity, $\sigma(v)$.
To review, the distribution function of the background plasma ions with the velocity expression in cartesian coordinates is
\[f_b(v_x, v_y, v_z) = \frac{1}{(2 \pi T/m_b)^{3/2}} \exp\left(-(v_x^2 + v_y^2 + v_z^2) / (2 T/m_b)\right).\]We can re-express this in cylindrical coordinates $(v_r, \phi, v_z)$:
\[f_b(v_r, \phi, v_z) = \frac{1}{(2 \pi T/m_b)^{3/2}} v_r \exp\left(-(v_r^2 + v_z^2) / (2 T/m_b)\right).\]The distribution function of the fast particles is
\[f_F(v_x, v_y, v_z) = \delta(v_x)\delta(v_y)\delta(v_z - v_F).\]First attempt, which ends in a 2D integration
The fusion rate coefficient is
\[\left<\sigma v\right> = \int \int \;f_b\; f_F \,v\, \sigma(v) d^3 v_b \; d^3 v_F\]where v is the relative velocity between the background particle and the fast particle.
After removing the trivial integrals over the fast particle distribution we’re still left with two velocity dimensions, plus the trivial azimuthal integral:
\[\left<\sigma v\right> = \frac{1}{(2 \pi v_{\mathrm{th}}^2)^{3/2}} \int_0^{2\pi}d\phi \int_0^{\infty}dv_r \int_{-\infty}^{\infty}dv_z v_r \exp\left(-(v_r^2 + v_z^2) / (2v_{\mathrm{th}}^2)\right) v \; \sigma(v),\]where the relative velocity $v = \sqrt{v_r^2 + (v_z - v_F)^2}$. (Here the $v_z$ refers unambiguously to the background particle $\hat{z}$ velocity). I’ve also abbreviated $T/m_b$ as the square of the “thermal velocity”, $v_\mathrm{th}^2$.
This expression still has two integrals, and the annoying square root expression. We can bring it down to a single integral.
Second (successful) attempt, transforming to integrate over spherical shells
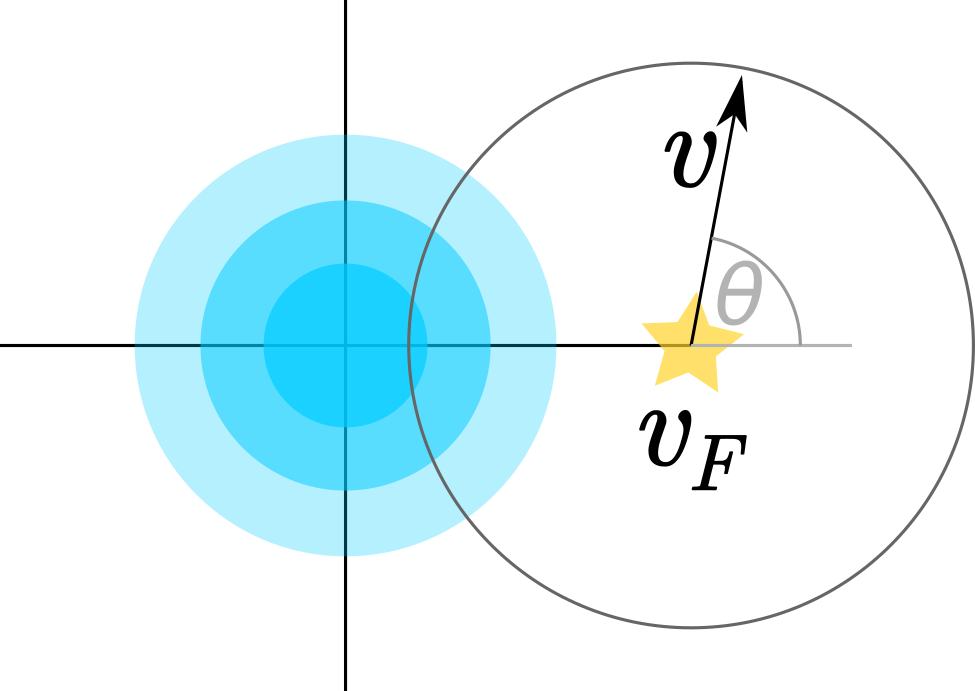
Instead of integrating over $\phi$, $v_r$ and $v_z$, we will transform to integrate over the background Maxwellian distribution in a spherical coordinate system centered at $v_F$. The angle $\phi$ is the same as before, but
\[\begin{align} v_z &= v_F + v \cos(\theta) \\ v_r &= v \sin(\theta) \\ \end{align}\]the expression of all space spanned by the integrals
\[\int_0^{2\pi}d\phi \,v_r \int_0^{\infty}dv_r \int_{-\infty}^{\infty}dv_z\]is the same as the space
\[\int_0^{2\pi}d\phi\,v \sin(\theta) \int_0^{\pi}d\theta\,v \int_0^{\infty}dv\]and the exponential in the integrand becomes
\[\begin{align} &\exp\left(-(v^2 \sin^2\theta + (v_F + v\cos(\theta))^2) / (2 v_\mathrm{th}^2)\right) \\ =&\exp\left(-(v^2 \sin^2\theta + v_F^2 + v^2\cos^2\theta + 2 v v_F \cos\theta) / (2 v_\mathrm{th}^2)\right) \\ =&\exp\left(-(v^2 + v_F^2 + 2 v v_F \cos\theta) / (2 v_\mathrm{th}^2)\right) \end{align}\](again, $T/m_b \to v_\mathrm{th}^2$)
leaving us with
\[\frac{1}{(2 \pi v_\mathrm{th}^2)^{3/2}} \int_0^{2\pi}d\phi\, \int_0^{\pi}d\theta\, \int_0^{\infty}dv\, v^2 \sin\theta\] \[\exp\left(-(v^2 + v_F^2 + 2 v v_F \cos\theta) / (2 v_\mathrm{th}^2)\right) v \; \sigma(v).\]Performing integrals
We can first do the trivial integral over $\phi$:
\[\begin{align} & \frac{2\pi}{(2 \pi T/m_b)^{3/2}} \int_0^{\pi}d\theta\, \int_0^{\infty}dv\, v^2 \sin\theta \\ & \exp\left(-(v^2 + v_F^2 + 2 v v_F \cos\theta) / (2 v_\mathrm{th}^2)\right) v \; \sigma(v). \\ \end{align}\]In order to prepare for integrating over $\theta$ we split this into a term with $\theta$ and a term without it \(=\exp\left(-(v^2 + v_F^2) / (2 v_\mathrm{th}^2)\right) \exp\left(-2 v v_F \cos\theta / (2 v_\mathrm{th}^2)\right)\)
so we have
\[\begin{align} \frac{2\pi}{(2 \pi v_\mathrm{th}^2)^{3/2}} & \int_0^{\infty}dv\,v^2\exp\left(-(v^2 + v_F^2) / (2 v_\mathrm{th}^2)\right) v \; \sigma(v) \\ & \int_0^{\pi}d\theta\, \sin\theta \exp\left(-2 v v_F \cos\theta / (2 v_\mathrm{th}^2)\right) \\ \end{align}\]The part over $\theta$ integrates cleanly to
\[2 \frac{\sinh(v\,v_F / v_\mathrm{th}^2)}{v \,v_F / v_\mathrm{th}^2}\]so we have
\[\left<\sigma v\right> = \frac{2}{(2 \pi v_\mathrm{th}^2)^{1/2}} \int_0^{\infty}dv\,v^2\exp\left(-(v^2 + v_F^2) / (2 v_\mathrm{th}^2)\right) v \; \sigma(v) \frac{\sinh(v\,v_F / v_\mathrm{th}^2)}{v \,v_F}.\]This is a success! We have reduced the expression to one integral over $v$, in which $v_F$ and $v_\mathrm{th}^2$ are parameters.
Just as a check, if we drop the $v \sigma(v)$ term, we should find that
\[1 = \frac{2}{(2 \pi v_\mathrm{th}^2)^{1/2}} \int_0^{\infty}dv\,v^2\exp\left(-(v^2 + v_F^2) / (2 v_\mathrm{th}^2)\right) \frac{\sinh(v\,v_F / v_\mathrm{th}^2)}{v \,v_F}.\]The integrand here is the probability mass in a spherical shell of radius $v$ and thickness $dv$ centered at a location $(0,0,v_F)$.
Practicality
For numerical evaluation, the $\sinh(x)$ term proves difficult when the beam energy is much larger than the temperature. I’ve had more success combining the exponential term with the sinh to get a difference of two exponentials.
\[e^{-(x^2 + y^2)/2}\frac{\sinh(x y)}{y} = \frac{1}{2 y}\left(e^{-(x-y)^2 / 2} - e^{-(x+y)^2 / 2}\right)\]($x, y$ are $v, v_F$ normalized by $v_\mathrm{th}$.)
At large $E_b / T$, the first term on the right hand side has almost all of the value.
Making the above substitution leads to the slightly cleaner formula
\[\left<\sigma v\right> = \frac{1}{\sqrt{2 \pi}} \frac{1}{v_\mathrm{th}\,v_F} \int_0^{\infty}dv\,v^2 \sigma(v) \left(e^{-(v - v_F)^2 / (2 v_\mathrm{th}^2)} - e^{-(v + v_F)^2 / (2 v_\mathrm{th}^2)}\right) .\]Limits
At $T \ll E_F$, the rate coefficient tends toward $v_F\,\sigma(E_F \mu / m_F)$: no integral necessary.
At very low (or zero) beam energy, $E_F \ll T$, the $1/v_F$ term becomes a problem. The exponential term can be replaced with its limit:
\[\lim_{y\to0} e^{-(x^2 + y^2)/2}\frac{\sinh(x y)}{y} = x e^{-x^2/2}\]Result
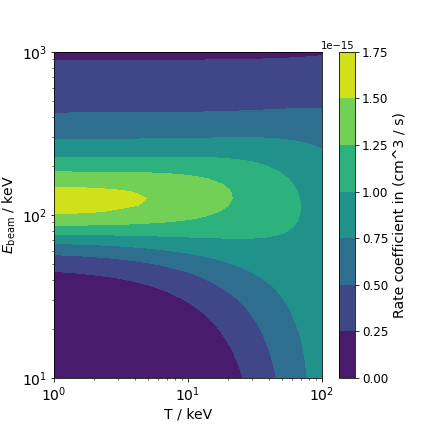
Figure 1 shows rate coefficients for deuterium beams on a tritium plasma target.