An ellipse's parallel curve: length, area, and torus volume.

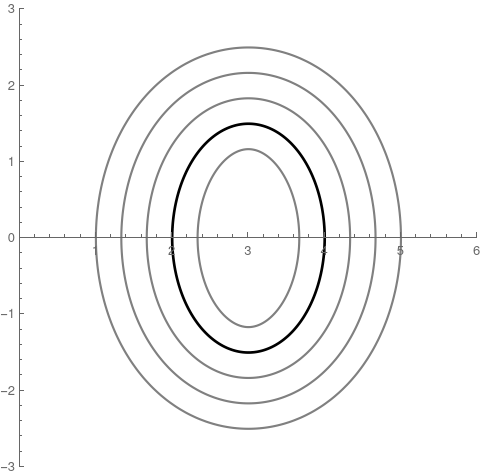
A parallel curve has a ‘fixed normal distance’ to a given curve. The parallel curve to an ellipse may be useful for modeling fusion systems: simple tokamak models are often considered as nested ellipses, but nested parallel curves might be more appropriate.

This post will explore some of the properties of parallel curves, especially those of ellipses.

Definition

A parallel curve is a relatively simple construction from a given curve in parametric form, $(x(t), y(t))$. The curve offset by distance $d$ is given by

\[x_d(t) = x(t) + d\, y'(t) / \sqrt{x'(t)^2 + y'(t)^2} \\ y_d(t) = y(t) - d\, x'(t) / \sqrt{x'(t)^2 + y'(t)^2}\]

For ellipses

For an ellipse defined by $x(t) = R_0 + a \cos(t)$, $y(t) = \kappa a \sin(t)$, $0\lt t \lt 2 \pi$,

\[x_d(t) = R_0 + \cos(t)\left(a + d\,\kappa / \sqrt{\kappa^2 \cos^2(t) + \sin^2(t)}\right) \\ y_d(t) = \sin(t)\left(a\,\kappa + d / \sqrt{\kappa^2 \cos^2(t) + \sin^2(t)}\right)\]

Length

The length of a curve parallel to a closed curve is equal to the length of the given curve plus $2 \pi d$. If you have a rope that tightly encircles the earth, how much longer would it need to be in order to keep a uniform distance of 1 meter from the ground?

Since the arc length of the ellipse is $\ell = 4 a E(1-\kappa^2)$, a parallel curve at distance $d$ has the arc length $\ell_d = 2 \pi d + 4 a E(1-\kappa^2)$.

Area enclosed by the parallel curve

Similarly, the area between the given ellipse and parallel curve can be described by a strip of length $P$ plus a circle of radius $d$. So, the total area enclosed is

\(A_d = \pi a^2 \kappa + 4 a d E(1-\kappa^2) + \pi d^2\).

Volume of a torus

If we sweep the parallel curve around the y axis to make a torus, the volume of the torus is

\[V_d = -\int_0^{\pi} 2 y_d(t) 2 \pi x_d(t) \frac{d x_d}{dt} dt\]

\(V_d = 2 \pi R_0 A_d = 2 \pi R_0 \left(\pi (d^2 + a^2 \kappa) + 4 a d E(1-\kappa^2)\right)\). Note that the simple relation \(V_d = 2 \pi R_0 A_d\) isn’t true for any shape swept around the centerline. It has to be left-right symmetrical around $R_0$.

Since the volume of the original torus is $2 \pi R_0 \pi a^2 \kappa$ the volume of the ‘parallel’ region alone is $ 2 \pi R_0 \left(\pi d^2 + 4 a d E(1-\kappa^2)\right)$.

Written on April 6th, 2021