Jacob Schwartz Scientist & HTML fan
Particles leaving a finite cylinder through the ends
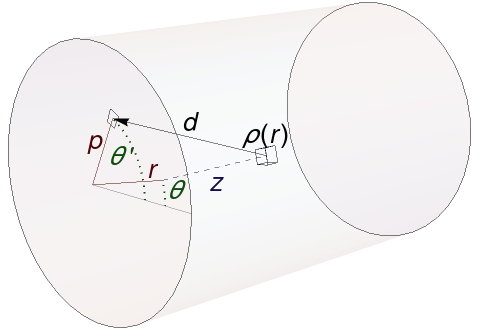
Several fusion start-up companies are proposing to use plasmas that can be approximated as a cylinder. These would be encapsulated in cylindrical chambers, perhaps with the ends open to handle the plasma in a ‘divertor’ configuration. Given a cylindrical plasma where the neutron source density depends only on $r$ (and not on $\theta$ or $z$), what fraction of the neutrons would leave the cylinder though the circular ends? This becomes a tricky integral, even for simple radial profiles. In this post we’ll see how far we can get analytically before switching to a numerical method.
Variable definitions
Let cylinder have radius 1 and length $A$. We will compute the fraction of neutrons leaving one circular face as a function of $A$. The coordinates on that face are $(p, \theta’)$, and the face is located at $z=0$. The coordinates of a source point within the cylinder will be called $(r, \theta, z)$. The neutron source density is $\rho(r)$.
Integrand
The distance from a volume element at $(r, \theta, z)$ and the surface element at $(p, \theta’)$ is
\[d = \left((p\cos\theta' - r \cos\theta)^2 + (p \sin \theta' - r \sin\theta)^2 + z^2\right)^{1/2},\]and by trigonometry, the cosine of the angle between the source-target vector and the surface normal is \(\cos(\phi) = \frac{z}{d}\). If the surface element’s normal is perpendicular to the neutron direction, it presents an infitesimal cross section; $\cos(\phi=\pi/2) = 0$.
All together, the fraction of neutrons from a volume element at $(r, \theta, z)$ which go on to impact the surface element at $(p, \theta’)$ is
\[\mathcal{I_0} = \frac{1}{4\pi} \frac{1}{d^2} \cos\phi = \frac{1}{4\pi} \frac{z}{\left((p\cos\theta' - r \cos\theta)^2 + (p \sin \theta' - r \sin\theta)^2 + z^2\right)^{3/2}}.\]The term ($1/4\pi$) assumes that neutrons are emitted isotropically from the source volume elements. The second term captures the decrease in flux from an element with the distance, and the third term captures the angular dependence.
The integral
The total flux through one circular end is
\[\mathcal{F} = \int_{-\pi}^{\pi}d\theta' \int_{0}^1 dp \int_0^1 dr\, \int_{-\pi}^{\pi} d\theta \int_0^A dz \; \mathcal{I_0} \,\rho(r) \, r\, p\]where the final $r$ and $p$ are the usual Jacobians for polar and cylindrical coordinates; since we’re integrating over $\theta’$ and $\theta$ we need both.
Since the final overall intensity is independent of $\theta’$ (the source is symmetric around the axis) we can make the problem a bit simpler by fixing $\theta’ = 0$.
First integration, $\theta’$
Since by construction the problem is symmetric around the axis, we can immediately remove the $\theta’$ integration by symmetry. We multiply the result by $2\pi$ and set $\theta’$ to 0, so the new integrand is
\[\mathcal{I_1} = \frac{1}{4\pi} \frac{z}{\left((p - r \cos\theta)^2 + (r \sin\theta)^2 + z^2\right)^{3/2}}.\]and
\[\mathcal{F} = 2 \pi \int_{0}^1 dp \int_0^1 dr\, \int_{-\pi}^{\pi} d\theta \int_0^A dz \; \mathcal{I_1} \,\rho(r) \, r\, p\]Second integration, $z$
The second integration is carried out over $z$.
\[\begin{align} \int_0^A dz \, \mathcal{I_1} &= \frac{1}{4 \pi} \int_0^A dz \; \frac{z}{\left((p - r \cos\theta)^2 + (r \sin\theta)^2 + z^2\right)^{3/2}} \\ \mathcal{I_2} &= \frac{1}{4\pi}\left( \frac{1}{\sqrt{r^2 + p^2 - 2 r p \cos\theta}} - \frac{1}{\sqrt{A^2 + r^2 + p^2 - 2 r p \cos\theta}} \right). \end{align}\]Third integration, $\theta$
The third integration is carried out over $\theta$:
\[\begin{align} \mathcal{I}_3 &= \int_{-\pi}^{\pi} d\theta \, \mathcal{I_2} \\ &= \frac{1}{4\pi} \left(\frac{4 K\left(\frac{4\,r\,p}{(r + p)^2}\right)}{r + p} - \frac{4 K\left(\frac{4\,r\,p}{\sqrt{A^2 + (r + p)^2}}\right)}{\sqrt{A^2 + \left(r + p\right)^2}}\right) \end{align}\]where $K(m)$ is the complete elliptic integral of the first kind.
Numerical integration, $r$ and $p$
We reacquaint ourselves with the full expression for the flux $\mathcal{F}$. There are only two integrals remaining, over $r$ and $p$.
\[\begin{align} \mathcal{F} &= 2\pi \int_0^1 \int_0^1 dr\,dp\,\mathcal{I}_3 \, \rho(r)\,r\,p \\ &= \frac{2\pi}{4\pi} 4 \int_0^1 \int_0^1 dr\,dp\, \left(\frac{K\left(\frac{4\,r\,p}{(r + p)^2}\right)}{r + p} - \frac{K\left(\frac{4\,r\,p}{\sqrt{A^2 + (r + p)^2}}\right)}{\sqrt{A^2 + \left(r + p\right)^2}}\right)\, \rho(r)\,r\,p \\ &= 2 \int_0^1 \int_0^1 dr\,dp\, \left(\frac{K\left(\frac{4\,r\,p}{(r + p)^2}\right)}{r + p} - \frac{K\left(\frac{4\,r\,p}{\sqrt{A^2 + (r + p)^2}}\right)}{\sqrt{A^2 + \left(r + p\right)^2}}\right)\, \rho(r)\,r\,p \end{align}\]This is a nice form for the expression as it is symmetric in $r$ and $p$, other than the radial source dependence $\rho(r)$. I have not found an analytic means to proceed further, even when $\rho(r)$ is a constant.
The shape of this integrand is shown below.
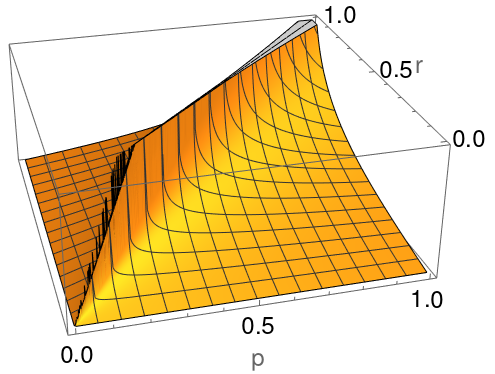
There is an infinite ridge at $r=p$. This is because $K(1) = \infty$ (a ComplexInfinity according to Mathematica). It is probably better from a numerical integration perspective to not have to traverse the infinite ridge, and instead stay only on one side. We can rewrite the integral’s bounds as
\[\begin{align} \mathcal{F} &= 2 \int_0^1 dp\, \int_0^p dr \, \left(\frac{K\left(\frac{4\,r\,p}{(r + p)^2}\right)}{r + p} - \frac{K\left(\frac{4\,r\,p}{\sqrt{A^2 + (r + p)^2}}\right)}{\sqrt{A^2 + \left(r + p\right)^2}}\right)\, \rho(r)\,r\,p \\ &+ 2 \int_0^1 dp\, \int_p^1 dr \, \left(\frac{K\left(\frac{4\,r\,p}{(r + p)^2}\right)}{r + p} - \frac{K\left(\frac{4\,r\,p}{\sqrt{A^2 + (r + p)^2}}\right)}{\sqrt{A^2 + \left(r + p\right)^2}}\right)\, \rho(r)\,r\,p \end{align}\]We’ve gone as far as we can go here. The next step is to compute the total neutron source rate; it’ll be the denominator in the expression for the fraction of neutrons leaving one end of the cylinder,
\(f_\mathrm{one-end} = \frac{\mathcal{F}}{\mathcal{S}}.\) where $\mathcal{S}$ is the total neutron source rate.
Total neutron source rate
The total source rate is
\[\mathcal{S} = \int_0^A dz \int_{-\pi}^{\pi} d\theta \int_0^1 dr \, \rho(r) r = 2 \pi A \int_0^1 r dr\, \rho(r).\]When $\rho(r)$ is a constant with $r$ this reduces to $\pi A \rho$.
Fraction of neutrons leaving either end
The quantity $f_\mathrm{one-end}$ is the computation of the fraction leaving one end; double it to get
\[\begin{align} f_\mathrm{either-end} &= 2 f_\mathrm{one-end} \\ &= \frac{ 4 \int_0^1 dp\, \int_0^1 dr \, \left(\frac{K\left(\frac{4\,r\,p}{(r + p)^2}\right)}{r + p} - \frac{K\left(\frac{4\,r\,p}{\sqrt{A^2 + (r + p)^2}}\right)}{\sqrt{A^2 + \left(r + p\right)^2}}\right)\, \rho(r)\,r\,p }{ \pi A \int_0^1 r dr\, \rho(r) } \end{align}\](For brevity I’ve combined the two halves of the numerator integration again.)
Results for various radial source distributions
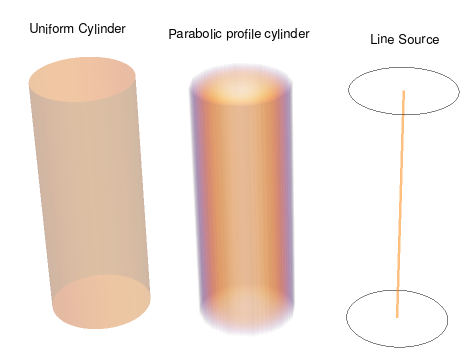
I’m not totally sure about this, but I think that for most cylindrical fusion machines, the neutron source strength would increase toward the plasma axis $(r=0)$. The radial dependence $\rho(r)$ would be between the extremes of a constant density (Figure 3 left) and a pure line source (right); a parabolic dependence (center) represents a ‘typical’ profile.
Figure 4 shows $f_\mathrm{body} \equiv 1 - f_\mathrm{either-end}$ evaluated for these three distributions.
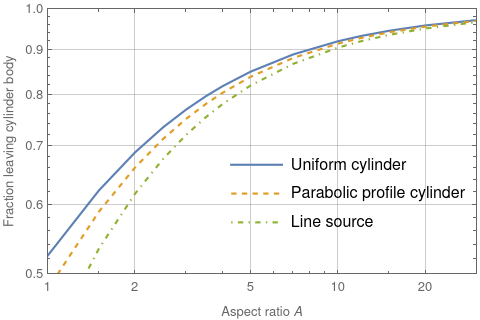
Note that the pure line source case is exactly solvable; $f_\mathrm{body,line} = \left(\sqrt{1 + A^2} - 1\right) / A$.
For $A \gt 5$ the results are all within 5% of one another. This is encouraging as with decently large $A$ we can estimate $f_\mathrm{body}$ fairly well even for an unknown source profile.
The Mathematica integration code is reproduced below:
ρ[r_] := 1
(* ρ[r_] := 1 - r^2 *)
fEitherEnd[A_?NumericQ] :=
NIntegrate[
2 p r ( EllipticK[4 p r/(p + r)^2]/(p + r) -
EllipticK[4 p r/(A^2 + (p + r)^2)]/Sqrt[
A^2 + (p + r)^2]) ρ[r], {r, 0, 1}, {p, 0, 1},
WorkingPrecision -> 10, Exclusions -> r==p] /
(π A NIntegrate[r ρ[r], {r, 0, 1}])
fBody[A_?NumericQ] := 1 - fEitherEnd[A]