Interaction of particles at depth in a slab

Motivation

This problem is explored in rough analogy to the problem of neutron deposition in the first wall of a fusion reactor. Of course, this lacks any number of complexities, but I’m interested in this set up as a very simple model.

Problem statement

There is a slab of material of thickness $a$. Above the slab is a gas of collisionless particles with an isotropic velocity distribution. When particles travel through the slab they are absorbed with some typical mean free path $\lambda.$ Of the particles that hit the slab, what fraction will be transmitted through it? (Pretend that the velocity distribution of the particles above the slab is not affected by the absorption in the material; that would become a much more difficult problem.) Also, what is the profile of the deposition of particles within the slab?

Solving the problem

Orient the slab normal to the z axis. Let the z axis be the polar axis for a spherical coordinate system in $\theta, \phi$. We will integrate over the behavior of particles coming from each angle in the upper half plane.

• The rate of particles in the gas encountering the plane is proportional to their motion in the z direction, $\cos\theta$.
• The distance that particles must travel through the material is $a/\cos\theta$.
• The fraction of particles not absorbed after travelling a distance $d$ through the material is $\exp(-d/\lambda)$.
• The differential solid angle is proportional to $\sin\theta$. (This is the standard Jacobian for spherical coordinate systems.)
• Integrate over the upper half plane, $0 \lt \theta \lt \pi/2$, and over all $\phi$.

Express this all as an integral. Normalize by an expression proportional to the rate of particles encountering the plane.

The transmission factor is \begin{equation} t = \frac{\int_0^{2 \pi} d\phi \int_0^{\pi/2} d\theta \sin \theta \cos\theta\, e^{-a/{\lambda \cos\theta}}}{\int_0^{2 \pi} d\phi \int_0^{\pi/2} d\theta \sin \theta \cos\theta}. \end{equation}

Simplify

The denominator evaluates to $\pi$, and the $\phi$ integral is $2\pi$, so we are left with a constant factor of $2$;

\[\begin{equation} t = 2\int_0^{\pi/2} d\theta \sin \theta \cos\theta\, e^{-a/{\lambda \cos\theta}}. \end{equation}\]

The integral can be simplified via u-subsitution, $u = \cos\theta$ and $du = -\sin\theta\,d\theta$. It becomes

\[\begin{equation} t = 2 \int_0^{1} u \,e^{-a/(\lambda u)} \; du. \end{equation}\]

A second substituion of $w = 1/u$ makes this into

\[\begin{equation} t = 2 \int_{1}^{\infty} \frac{1}{w^3} e^{-w (a/\lambda)} \;dw. \end{equation}\]

This matches the definition of the generalized exponential integral, the $\mathrm{E}_n$-function, \(\mathrm{E}_n(x) = \int_{1}^\infty \frac{e^{-t x}}{t^n} \; dt\). In Mathematica it is implemented as ExpIntegralE[n,x].

Solution

\(\begin{equation} t\left(\frac{a}{\lambda}\right) = 2 \,\mathrm{E}_3\left(\frac{a}{\lambda}\right) \tag{1}\label{eq:one} \end{equation}\) This expression is normalized so that a thin slab has $t = 1$.

The deposition profile

\[\begin{equation} d(a, \lambda) = 2 \frac{1}{\lambda} \mathrm{E}_2\left(\frac{a}{\lambda}\right) \end{equation}\]

is the derivative of the transmission profile: \((d/dx) \mathrm{E}_{n} = \mathrm{E}_{n-1}\). This has the same normalization, and the integral of the deposition in a very thick slab is unity.

Alternate construction of the deposition profile

One can also directly integrate to find the deposition profile. The deposition per unit length is $\frac{1}{\lambda}e^{-x/\lambda}$ and particles at an angle $\theta$ stay around a given depth $da$ for a length proportional to $1/\cos\theta$. This cancels out the $\cos\theta$ in the numerator, so the integral becomes

\[\begin{equation} d(a, \lambda) = 2 \int_0^{\pi/2}d\theta\, \sin\theta \frac{1}{\lambda} e^{-a/\lambda \cos\theta}. \end{equation}\]

This can be evaluated in the same manner, but it’s simpler; it becomes proportional to $\int e^{-w}/w^2 \;dw$.

Characteristics of the solution

The first figure shows the transmission curve, as well as short- and long-range asymptotics.

For small $a/\lambda$ the transmission goes like $\exp(-2a/\lambda)$. This is neat because in the 1D version of the problem, the exact solution would be $\exp(-a/\lambda)$. Transmission falls off roughly twice as fast for this 3D version. For large $a/\lambda$ transmission is approximately $2\exp(-a/\lambda)/(a/\lambda)$: the exponential now has the same falloff as the 1D problem. At long ranges, only particles with directions close $\theta=0$ contribute, so it’s almost like 1D.

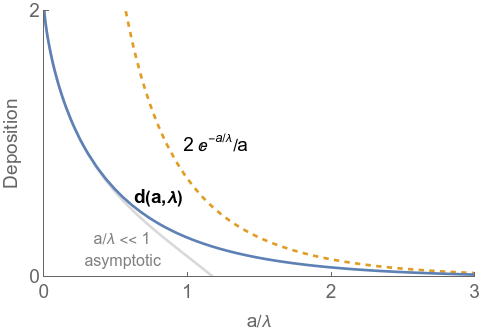
The second figure shows deposition in the slab. This has a similar long-range asymptotic, but the derivative of this function becomes infinite as $a\to\infty$. A good short-range approximation is $\frac{1}{\lambda}\left(2-2(1-\gamma)\frac{a}{\lambda}-\frac{a^2}{\lambda ^2}+2 \frac{a}{\lambda}\log \left(\frac{a}{\lambda }\right)\right)$ where $\gamma$ is the Euler constant.

Relation to other posts

This problem is similar to the one in my first post. The geometry is the same (if inverted) but now I’ve averaged over the distribution of particles that encounter a surface. The solution is also in terms of ExpIntegralE.

Written on April 14th, 2024