Magnetic field at the surface of a long conductor with a square cross section

Assume an infinite conductor with a square cross-section. It has side length $l$ and carries a current along its length with uniform density $J$.

At the corner of a square, the magnitude of the field is

\[\left|B\right| = J l \mu_0 \frac{\pi + \log(4)}{4 \sqrt{2} \pi} = 0.2548 J l \mu_0\]

In the middle of a side,

\[B = J l \mu_0 \frac{2 \arctan(1/2) - \log(5)/2}{2\pi} = 0.2756 J l \mu_0\]

Anywhere along a side, with $0 < x < 1$,

\[\begin{split} \left|B\right| &=\frac{J l \mu }{2 \pi } \biggl\{ \biggl[\cot ^{-1}(1-x)+x \left(-\pi +\tan ^{-1}(1-x)+\tan ^{-1}(x)\right)+\\ &\qquad\qquad\qquad\tanh ^{-1}\left(\frac{1-2 x}{3+2 (-1+x) x}\right)\biggr]^2+ \\ &\qquad\quad \frac{1}{4} \biggl[2 \tan ^{-1}(1-x)+2 \tan ^{-1}(x)+x \left(\log \left(x^{-2}+1\right)\right)+ \\ &\qquad\qquad\qquad (-1+x) \log \left(1-\frac{1}{2+(-2+x) x}\right)\biggr]^2 \biggr\}^{\!1/2}. \end{split}\]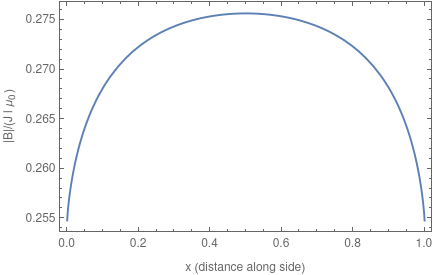

Is there a nice formula for the field strength at the corner of a polygonal conductor?

Written on October 21st , 2020